Гармонические колебания.

Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями.

Например, в случае механических гармонических колебаний:.

В этих формулах ω – частота колебания, x_m – амплитуда колебания, φ₀ и φ₀’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ₀’ = φ₀ +π/2 полностью совпадают.

Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0  смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ₀’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=х_m, следовательно, удобнее пользоваться функцией cos и φ₀=0.

Выражение, стоящее под знаком cos или sin, наз. фазой колебания: .

Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.

Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).

Скорость и ускорение при гармонических колебаниях.

Согласно определению скорости, скорость – это производная от координаты по времени 

Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2.

Величина  - максимальная скорость колебательного движения (амплитуда колебаний скорости).

Следовательно, для скорости при гармоническом колебании имеем: ,  а для случая нулевой начальной фазы  (см. график).

Согласно определению ускорения, ускорение – это производная от скорости по времени:

 - вторая производная от координаты по времени. Тогда: .

Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе).

Величина 

- максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: , а для случая нулевой начальной фазы:  (см. график).

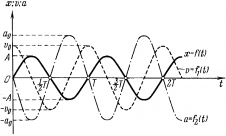
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).

Сравним выражения для смещения и ускорения при гармонических колебаниях:

   и    .

Можно записать:  -

т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.

Часто бывает удобно записывать уравнения для колебаний в виде: ,

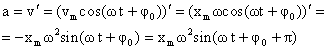где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: . Аналогично для скорости и ускорения.