Электромагнитные колебания

ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.

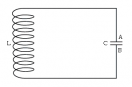
Периодические изменения во времени электрического заряда (силы тока, напряжения) называются электромагнитными колебаниями.

Электрическая цепь, состоящая из последовательно соединенных конденсатора с емкостью C  и катушки с индуктивностью L, наз. колебательным контуром.

Если активное сопротивление R → 0, то колебания являются свободными незатухающими. Возбудить колебания в контуре можно либо сообщив заряд конденсатору (электрическое поле), либо с помощью электромагнитной индукции возбудив ток в катушке (магнитное поле).

Закономерности электромагнитных и механических колебаний математически одинаковы.

Общий вид уравнения колебательного движения: .

Уравнение гармонического колебания заряда (изменение величины электрического заряда!): .

Колебания тока: , т.о.  .

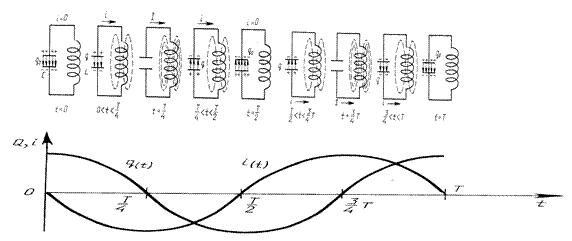
В колебательном контуре происходят периодические превращения энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно.

Для энергии электрического поля конденсатора воспользуемся выражением , а для энергии магнитного поля катушки .

Запишем закон сохранения энергии и возьмем производную от левой и правой частей уравнения: .

Т.к. производная от постоянной величины равна нулю, то

.

Производная суммы равна сумме производных:  и .

Следовательно: , а значит .

Т.о. получим:  и      - формула Томсона.

Из закона сохранения энергии следует:  и, следовательно, 

В случае затухающих колебаний коэффициент затухания   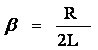и