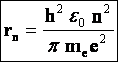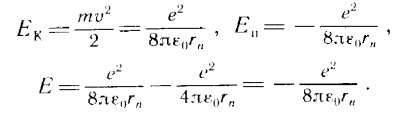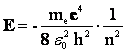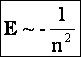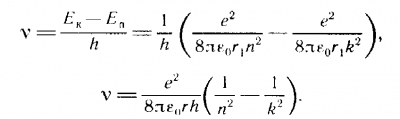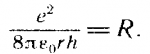Спектральные закономерности. Постулаты Бора.

Спектральные закономерности
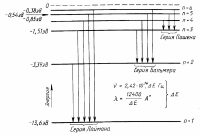
В середине XVIII в. Г. Кирхгоф обнаружил: свечение газов дает четко выраженные дискретные линии. Швейцарский преподаватель И. Бальмер эмпирически вывел формулу для спектра водорода (1885): , где п—любое целое число >2, т. е. п=3, 4, 5 и т.д.
Величина R носит название "постоянная Ридберга"
Для инфракрасной области спектра аналогичную формулу вывел Ф. Пашен: , где п—любое целое число >3, т. е. п=, 4, 5 и т.д.
А для ультрафиолетовой - Т. Лайман , где п—любое целое число >1, т. е. п=2,3, 4, 5 и т.д.
Значения длин волн спектральных линий, вычисленных по этим формулам, совпадали с исключительной точностью со значениями длин волн этих линий, измеренных экспериментально. В конце XIX в. ученые обнаружили фундаментальную закономерность в микромире, которую в то время объяснить не смогли. Только через 30 лет Н. Бор дал физическую интерпретацию этой формулы. Он предположил, что два члена в формуле Бальмера представляют собой полные энергии разрешенных орбит электрона в атоме водорода.
Преобразовав формулу Бальмера (умножив обе части на h), получим:
Учитывая, что согласно гипотезе Планка энергия кванта Δ, получим:
Свои постулаты Н. Бор применил для построения теории атома водорода.
Постулаты Бора
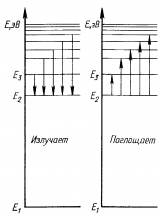
1. Атомная система может находиться только в особых стационарных квантовых состояниях, каждому из которых соответствует определенная энергия Е_n . В стационарном состоянии атом не излучает.
2. При переходе атома из стационарного состояния с большей энергией E_k в стационарное состояние с меньшей энергией E_n излучается квант энергии:
3. К этим постулатам следует добавить правило квантования орбит: в стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные, квантованные значения момента импульса где r_n - радиус n-ой орбиты; v_n—скорость электрона на этой орбите; m_e— масса электрона, п—целое число - номер орбиты или главное квантовое число.
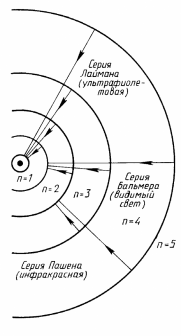
Модель атома водорода по Бору
На электрон со стороны ядра действует кулоновская сила, сообщая ему центростремительное ускорение. Поэтому

Из правила квантования: Подставляя уравнение для скорости электрона на орбите в предыдущее, получим: , где n=1,2,3...
Если п=1, а r₁=0,5-10^-10 м, то r₂=r₁^.n²=4r₁, r₃=9r₁ и т.д. Т.о. или r_n~n².
Полная энергия атома равна: Е = E_k + E_п
Подставляя выражение для радиуса стационарной орбиты, получим: Знак "-" говорит о том, что между электроном и ядром действуют силы притяжения.
Переход электрона с более высокой орбиты k на орбиту п сопровождается излучением фотона с частотой: Таким образом, мы пришли к формуле Бальмера, где - постоянная Ридберга.
Трудности теории Бора Правило квантования Бора применимо не всегда, представление об определенных орбитах, по которым движется электрон в атоме Бора, оказалось условным. Теория Бора неприменима для многоэлектронных атомов и не объясняет ряд спектральных закономерностей.
В 1917 г. А. Эйнштейн предсказал возможность перехода атома с высшего энергетического состояния в низшее под влиянием внешнего воздействия. Такое излучение называется вынужденным излучением и лежит в основе работы лазеров.
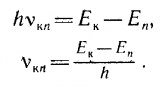
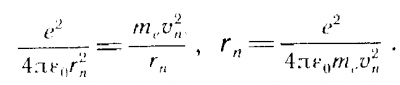
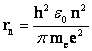